1 / 20

Which statement, about an aeroplane leaving ground effect at constant angle of attack, is correct?

I. The lift coefficient CL remains constant.
II. The induced drag coefficient CDI decreases.

  • A
    I is incorrect, II is incorrect.
  • B
    I is correct, II is correct.
  • C
    I is correct, II is incorrect.
  • D
    I is incorrect, II is correct.

Refer to figure 1 and figure 2.

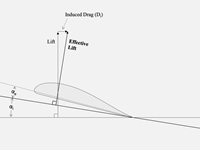
In figure 1 you can see the effect of downwash on the effective angle of attack and therefore the induced drag of a wing profile.Now the question is asking what will happen to the induced drag coefficient and the lift coefficient when leaving ground effect:

  • Induced drag coefficient: Using figure 1, and knowing that when leaving ground effect the downwash increases, we know that our induced angle (αi) will increase, therefore increasing the induced drag (DI). This means an increase in CDI, hence statement 2 is incorrect!
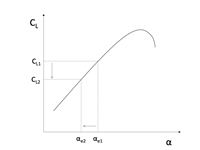
  • Lift coefficient: Using figure 1, and knowing that when leaving ground effect, the effective angle of attack (αe) decreases because of the increased downwash, we can see in figure 2 that a decrease in effective angle of attack will decrease the coefficient of lift of the wing. Therefore we can say that statement 1 is incorrect!

Your Notes (not visible to others)



This question has appeared on the real examination, you can find the related countries below.

Keyboard Shortcut Use Keyboard Shortcuts